Dans ma discussion ici, je suppose que votre $ \ theta $ est effectivement une longitude et $ \ phi $ est effectivement une latitude. Peut-être que les coordonnées sphériques plus typiques utilisent un angle descendant du pôle nord plutôt que vers le haut de l'équateur et inversent les rôles des deux symboles à partir de cela - mais ce n'est pas un problème de le gérer de toute façon, donc je m'en tiendrai à ce que votre notation semble être.

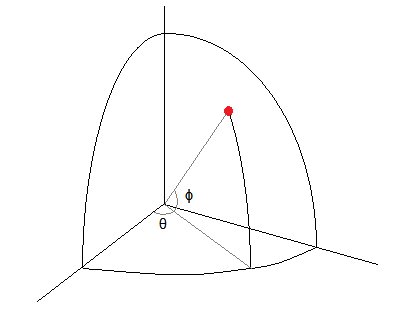
Notez que la distribution du rayon n'a pas d'intérêt ici, seulement les angles, donc nous pourrions projeter tout sur une sphère unitaire sans changer les angles. Ceci est assez utile dans le cas normal.

Avec une distribution sphérique symétrique comme la normale standard tridimensionnelle, l'apparence de la distribution de l'inclinaison est liée au fait qu'il y a beaucoup plus de surface sur la surface d'une sphère près de l'équateur que près des pôles.

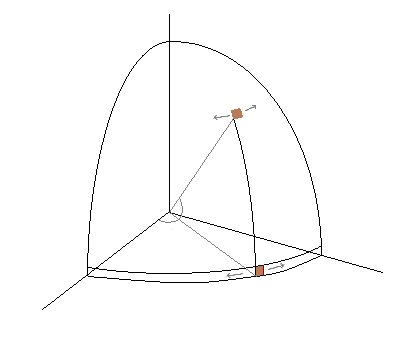
Si vous suivez les mathématiques (ou écrivez un argument géométrique en termes d'éléments de probabilité similaire à la question 2D précédente), vous pouvez obtenir que l'inclinaison doit avoir une densité proportionnelle à $ \ cos (\ phi) $. Voici un argument géométrique qui devrait le motiver dans les termes "éléments de probabilité":

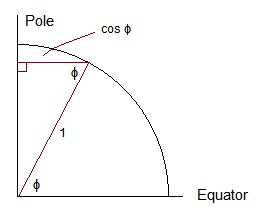
Puisque le rayon à l'équateur est 1 et le rayon à la latitude $ \ phi $ est $ \ cos (\ phi) $, la circonférence à la latitude $ \ phi $ est proportionnelle à $ \ cos (\ phi) $, et donc la densité à $ \ phi $ est proportionnelle à $ \ cos (\ phi) $.

Cas uniforme : Avec l'uniforme 3D normalisé à rayon constant, vous n'avez pas l'uniformité de densité sur la sphère pour la même raison que nous ne l'avons pas fait dans le cas 2D - lorsque vous projetez sur la sphère, il y a beaucoup plus de «densité» sur la sphère près des angles où se trouvent les coins que là où se trouvent les côtés (avec des parties proches du milieu de les bords étant entre les deux) - car il y a plus de volume du cube pour les angles proches des coins que pour les angles proches du milieu des faces.

Nous pouvons le voir en générant de nombreuses valeurs aléatoires uniformément dans le cube et en les projetant sur la sphère. Puisqu'il y a plus de volume près des coins que près des faces du cube, il y a une plus grande densité regardant «vers l'intérieur» depuis les coins que les faces. Si nous traçons la hauteur (rappelez-vous qu'il s'agit d'une valeur z projetée, $ z ^ * = z / r $, où $ r = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2} $) au-dessus de l'équateur par rapport à la longitude, nous obtenons le graphique du haut ci-dessous:

Cette hauteur correspond au côté vertical du triangle rectangle dans le diagramme précédent ; cette hauteur est le $ \ sin $ de $ \ phi $ ($ z ^ * = \ sin (\ phi) $). Pour convertir cela en latitude ($ \ phi $), nous prendrions l'arcsin de cette hauteur verticale projetée, ce que nous voyons dans le graphique inférieur. Cela "étire" les choses plus on se rapproche du pôle, ce qui fait chuter la densité en fonction de la latitude à 0 au pôle nord et sud (à la fois pour l'uniforme et pour le cas normal).

La densité pour $ \ phi $ sera alors l'intégrale de cette densité bivariée sur $ \ theta $.

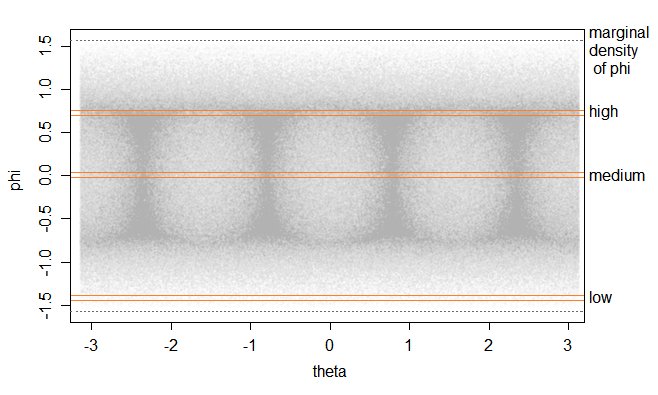
En regardant le marginal pour $ \ theta $ (c'est-à-dire des bandes descendant à des valeurs fixes de $ \ theta $) donne quatre pics dans la densité de $ \ theta $ comme vous le remarquez - en effet, cela découle directement du cas 2D, mais comme nous le voyons maintenant, cela donne également une paire de pics dans la densité de $ \ phi $ loin de l'équateur, correspondant à une région sur la surface de la sphère unitaire où les coins et les bords supérieur / inférieur du cube se projettent.

La distribution cumulative complémentaire pour la latitude sphérique $ \ phi $ donne la chance qu'un point aléatoire dans le cube $ [- 1,1] ^ 3 $ se trouve au-dessus du cône qui représente la fonction $ z = \ cot ( \ phi) \ sqrt {x ^ 2 + y ^ 2} $. Étant donné que ces points sont uniformément répartis dans tout le cube (qui a un volume de 8 $), cette chance est un huitième du volume entre le cône et le sommet du cube. Lorsque la latitude dépasse $ \ pi / 4 $, ce volume est celui d'un cône droit de hauteur $ 1 $ et de base $ \ cot (\ phi) $, égal à

$$ F _ {+} ( \ phi) = \ frac {1} {8} \ frac {\ pi} {3} \ cot ^ 2 (\ phi). $$

Voir les deux tracés de droite sur la figure.

Lorsque la latitude est inférieure à $ \ arctan (1 / \ sqrt {2}) $, c'est le volume de l'intersection d'un cône semi-infini et du cube. Une intégration en coordonnées polaires donne l'expression

$$ F _ {-} (\ phi) = \ frac {1} {8} \ left (4- \ frac {4} {3} \ tan ( \ phi) \ left (\ sqrt {2} +2 \ tanh ^ {- 1} \ left (\ tan \ left (\ frac {\ pi} {8} \ right) \ right) \ right) \ right). $$

Voir les deux graphiques les plus à gauche de la figure.

Les dérivées négatives de ces expressions donnent le densité. Entre $ \ arctan (1 / \ sqrt {2}) \ approx \ pi / 5 $ et $ \ pi / 4 $ se trouve une région de transition où l'intersection du cône avec le cube est compliquée. Bien qu'une expression exacte puisse être développée, elle serait compliquée. Ce que nous savons, c'est que la densité doit changer continuellement de la dérivée de $ -F _ {-} $ à la dérivée de $ -F _ {+} $ car $ \ phi $ varie entre ces points. Ceci est montré dans un histogramme d'un million de valeurs simulées (à partir de la moitié supérieure du cube uniquement - la moitié inférieure sera une image miroir). La courbe d'or est le graphique de $ - \ frac {d} {d \ phi} F _ {-} $ tandis que la courbe rouge à droite est le graphique de $ - \ frac {d} {d \ phi} F _ {+ }. $

Ceci clarifie pourquoi les modes ne sont pas à $ \ phi = \ pm \ pi / 4 $, mais doivent mentir entre ces valeurs et $ \ pm \ arctan (1 / \ sqrt {2}) $.