Normalement, vous n'appelleriez pas la valeur observée une "valeur estimée".
Cependant, malgré cela, la valeur observée est néanmoins techniquement une estimation de la moyenne à son $ x $ particulier, et la traiter comme une estimation nous dira en fait le sens dans lequel OLS est meilleur pour estimer la moyenne là-bas.
De manière générale, la régression est utilisée dans le cas où si vous preniez un autre échantillon avec les mêmes $ x $, vous n'obtiendriez pas les mêmes valeurs pour les $ y $. Dans la régression ordinaire, nous traitons les $ x_i $ comme des quantités fixes / connues et les réponses, les $ Y_i $ comme des variables aléatoires (avec des valeurs observées notées $ y_i $).
En utilisant une notation plus courante, nous écrivons
$$ Y_i = \ alpha + \ beta x_i + \ varepsilon_i $$
Le terme de bruit, $ \ varepsilon_i $, est important car les observations ne sont pas correctes sur la ligne de population (s'ils le faisaient, il n'y aurait pas besoin de régression; deux points quelconques vous donneraient la ligne de population); le modèle pour $ Y $ doit tenir compte des valeurs qu'il prend, et dans ce cas, la distribution de l'erreur aléatoire tient compte des écarts par rapport à la ligne ('vraie').
L'estimation de la moyenne au point $ x_i $ pour la régression linéaire ordinaire a une variance
$$ \ Big (\ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} \ Big) \, \ sigma ^ 2 $$
tandis que l'estimation basée sur la valeur observée a une variance $ \ sigma ^ 2 $.
Il est possible de montrer que pour $ n $ au moins 3, $ \, \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} $ n'est pas supérieur à 1 (mais il peut être - et en pratique est généralement - beaucoup plus petit). [De plus, lorsque vous estimez l'ajustement à $ x_i $ par $ y_i $, il vous reste également la question de savoir comment estimer $ \ sigma $.]
Mais plutôt que de poursuivre la démonstration formelle, réfléchissez un exemple qui, je l’espère, sera plus motivant.
Soit $ v_f = \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum ( x_i- \ bar {x}) ^ 2} $, le facteur par lequel la variance d'observation est multipliée pour obtenir la variance de l'ajustement à $ x_i $.
Cependant, travaillons sur l'échelle de l'erreur standard relative plutôt que sur la variance relative (c'est-à-dire, regardons la racine carrée de cette quantité); les intervalles de confiance pour la moyenne à un $ x_i $ particulier seront un multiple de $ \ sqrt {v_f} $.
Donc à l'exemple. Prenons les données cars dans R; ce sont 50 observations collectées dans les années 1920 sur la vitesse des voitures et les distances parcourues pour s'arrêter:
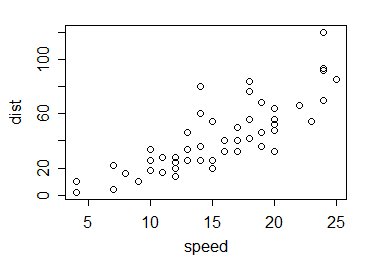
Alors, comment font les valeurs de $ \ sqrt {v_f} $ comparer avec 1? Comme ceci:
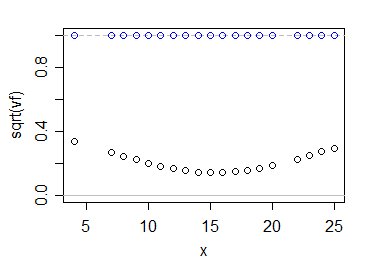
Les cercles bleus montrent les multiples de $ \ sigma $ pour votre estimation, tandis que les noirs le montrent pour l'estimation habituelle des moindres carrés. Comme vous le voyez, l'utilisation des informations de toutes les données rend notre incertitude quant à l'emplacement de la moyenne de la population considérablement plus petite - du moins dans ce cas, et bien sûr étant donné que le modèle linéaire est correct.
En conséquence , si nous traçons (disons) un intervalle de confiance à 95% pour la moyenne de chaque valeur $ x $ (y compris à des endroits autres qu'une observation), les limites de l'intervalle aux divers $ x $ sont généralement petites par rapport aux variation dans les données:
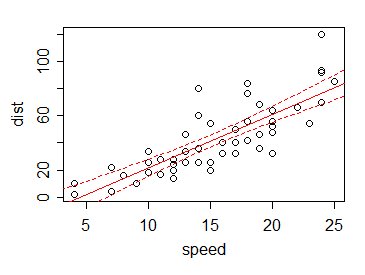
C'est l'avantage d'emprunter des informations à partir de valeurs de données autres que la valeur actuelle.
En effet, nous pouvons utiliser les informations d'autres valeurs - via la relation linéaire - pour obtenir de bonnes estimations de la valeur à des endroits où nous n'avons même pas de données. Considérez qu'il n'y a pas de données dans notre exemple à x = 5, 6 ou 21. Avec l'estimateur suggéré, nous n'avons aucune information - mais avec la droite de régression, nous pouvons non seulement estimer la moyenne à ces points (et à 5,5 et 12,8 et ainsi de suite), nous pouvons lui donner un intervalle - bien que, encore une fois, celui qui repose sur l'adéquation des hypothèses de linéarité (et de variance constante des $ Y $ s, et de l'indépendance).