TL; DR: Ne confondez pas la densité de probabilité avec la probabilité. Dans l'exemple donné, la probabilité est nulle: $ \ mathrm {Pr} (m = 120 \, \ mathrm {g}) = 0 $ , mais la probabilité densité est différente de zéro: $ p_M (m = 120 \, \ mathrm {g}) \ approx 0.0299 \, \ mathrm {g ^ {- 1} } $ .
Il y a déjà eu pas mal de réponses, mais je pense que visualiser les choses pourrait aider à comprendre, ici.
Je suis d'accord avec les commentaires d'Itamar Mushkin au PO qu'il y a probablement une certaine confusion de probabilité (écrivons-le comme $ \ mathrm {Pr} (m ) $ ) et la densité de probabilité (écrivons-le comme $ p_M (m) $ ), qui n'a été correctement abordée dans aucune des réponses, encore.
Réponse complète
Dans la vidéo, une distribution normale avec une moyenne $ \ mu = 112 \, \ mathrm {g} $ et un écart type $ \ sigma = 9 \, \ mathrm {g} $ est utilisé comme une fonction de densité de probabilité (généralement abrégée par "pdf"). Appelons $ p_M (m) $ le pdf de la variable aléatoire $ M $ (notre masse de glace ), tel que:
$$
p_M (m) = \ mathcal {N} (\ mu = 112 \, \ mathrm {g}, \ sigma = 9 \, \ mathrm {g}) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {\ frac {- (m- \ mu) ^ 2} {2 \ sigma ^ 2}}
$$
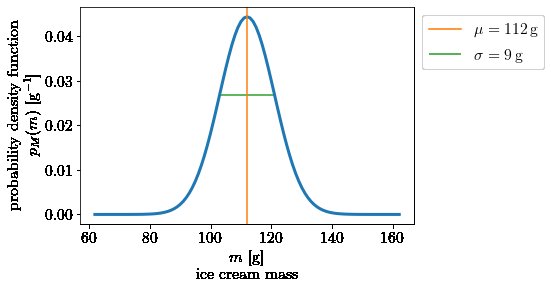
Notez (et c'est crucial!), comment la densité de probabilité $ p $ est not dimensionless, mais a des unités de $ \ mathrm {g ^ {- 1}} $ , puisqu'il s'agit d'un density, c'est-à-dire qu'il donne la probabilité par intervalle de masse . Notez en outre que la densité de probabilité est non nulle pour toute masse finie (probabilité densité $ p_M $ , pas de probabilité $ \ mathrm {Pr} $ !). Lorsque nous parlons couramment de densités, nous nous référons généralement à la masse par volume, par ex. la densité d'un diamant est d'environ 3,51 $ \, \ mathrm {g / cm ^ 3} $ . Ici, quand on parle de densité de probabilité , la probabilité prend le rôle de la masse du diamant et l'intervalle de masse de la crème glacée prend le rôle du volume du diamant, donnant des unités de probabilité par masse.
Maintenant, pour arriver à une probabilité réelle, nous devons essentiellement multiplier la probabilité densité par un intervalle de masse $ \ Delta m = m_2-m_1 $ (de la même manière que nous aurions besoin de multiplier la densité du diamant par le volume du diamant pour obtenir la masse du diamant). Je dis en gros, parce que la bonne façon de le faire est d'intégrer le pdf sur cet intervalle de masse, ce qui vous donne l'aire sous la courbe (et l'aire sous une courbe consiste essentiellement à multiplier l'intervalle x par l'intervalle y en fines bandes):
$$
\ begin {align}
\ mathrm {Pr} (M \ in [m_1, m_2])
& = \ int_ {m_1} ^ {m_2} p_M (m) \, dm \ tag {1} \\
& = P_M (m) | _ {m_1} ^ {m_2} \\
& = P_M (m_2) - P_M (m_1) \ tag {2}
\ end {align}
$$
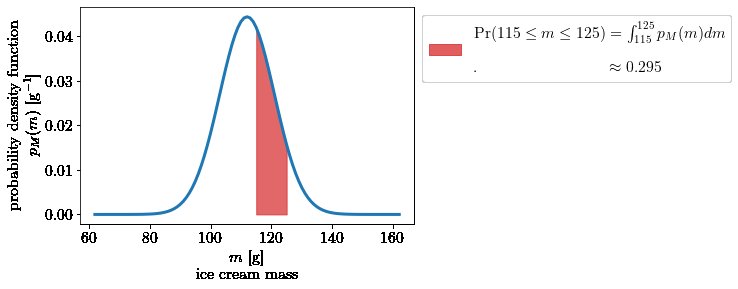
Dans la formule ci-dessus, $ P_M (m) $ est la fonction de distribution cumulative (généralement abrégée en cdf et que Henry appelait $ \ Phi $ dans sa réponse), qui est l'intégrale du pdf:
$$
\ begin {align}
P_M (m)
& = \ int _ {- \ infty} ^ m p_M (\ tilde {m}) \, d \ tilde {m} \\
& = \ mathrm {Pr} (M \ le m)
\ end {align}
$$
Ainsi, le cdf vous donnerait directement la réponse à la question: "Quelle est la probabilité que la glace ait une masse d'au moins une masse $ m $ ? " Et la réponse serait non nulle.
L'image correspondante pour $ \ mathrm {Pr} (M \ in [m_1, m_2]) $ en termes de cdf est la suivante:
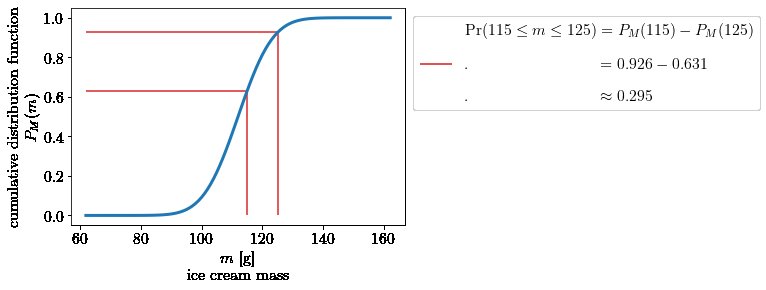
Jusqu'ici tout va bien, c'est le point de départ de la plupart des autres réponses, dont beaucoup donnent des exemples pour comprendre intuitivement pourquoi la probabilité que la masse prenne une valeur spécifique passe à zéro.
Pour répondre à cette question, ici, avec les images et les équations ci-dessus: Si vous voulez connaître la probabilité que la masse prenne une valeur exacte, par exemple $ m_ \ ast = 120 \, \ mathrm {g} $ , vous pourriez jeter un œil à l'équation (1) et à la deuxième image et vous en rendre compte en regardant $ \ mathrm {Pr} (M = m_ \ ast) $ vous envoyez effectivement vos deux limites d'intégration à la même masse $ m_1, m_2 \ rightarrow m_ \ ast $ qui envoie l'intervalle de masse à zéro $ \ Delta m = m_2 - m_1 \ rightarrow 0 $ , et donc l'aire sous la courbe sera égale à zéro: $ \ int_ {m_1 \ rightarrow m_ \ ast} ^ {m_2 \ rightarrow m_ \ ast} p_M (m) \, dm \ rightarrow 0 $ . De manière équivalente, vous pouvez regarder l'équation (2) et voir directement que: $ P_M (m_2 \ rightarrow m_ \ ast) - P_M (m_1 \ rightarrow m_ \ ast) \ rightarrow 0 $ .
N Remarque, la probabilité que la masse soit exactement $ m_ \ ast = 120 \, \ mathrm {g} $ passe à zéro : $ \ mathrm {Pr} (M = 120 \, \ mathrm {g}) = 0 $ , la densité de probabilité à la masse $ m_ \ ast = 120 \, \ mathrm {g} $ n'est pas zéro: $ p_M (m = 120 \, \ mathrm {g}) \ environ 0,0299 \, \ mathrm {g ^ {- 1}} $ .
Code
Pour ceux qui s'intéressent au code python qui a généré les images ci-dessus:
importer numpy comme np
importer matplotlib.pyplot comme plt
depuis la norme d'importation scipy.stats
depuis scipy.integrate import quad
mu = 112 # moyenne
sigma = 9 # écart type
norm = norm (loc = mu, scale = sigma) # distribution normale
p = norm.pdf # fonction de densité de probabilité
P = norm.cdf # fonction de distribution cumulative
m = np.linspace (mu-5 * sigma, mu + 5 * sigma, 10 * sigma + 1) # gamme de masse de crème glacée
################################################ #############################
# graphique de la fonction de densité de probabilité (pdf)
################################################ #############################
fig = plt.figure ()
plt.plot (m, p (m), lw = 3)
plt.axvline (mu, color = 'C1', label = " $ \ mu =% d \, \ mathrm {g} $ "% mu)
plt.hlines (p (norm.ppf ((1-0.6827) / 2)), xmin = mu-sigma, xmax = mu + sigma, couleur = 'C2',
label = " $ \ sigma =% d \, \ mathrm {g} $ "% sigma)
plt.legend (bbox_to_anchor = (1, 1), loc = 'en haut à gauche')
plt.xlabel (" $ m $ $ \ mathrm {[g]} $ \ n crème glacée ")
plt.ylabel ("fonction de densité de probabilité \ n $ p_M (m) $ $ [\ mathrm {g ^ {- 1 }}] $ ")
plt.show ()
################################################ #############################
# parcelle montrant la zone sous pdf correspondant à Pr (m1 < = m < = m2)
################################################ #############################
m1 = 115 # limite de masse inférieure
m2 = 125 # limite de masse supérieure
Delta_m = np.linspace (m1, m2, int (m2 - m1)) # intervalle de masse
fig = plt.figure ()
plt.plot (m, p (m), lw = 3)
plt.fill_between (Delta_m, 0, p (Delta_m), couleur = 'C3', alpha = 0.7,
label = " $ \ mathrm {Pr} (% d \ le m \ le% d)"
"= \ int _ {% d} ^ {% d} p_M (m) dm $ \ n \ n"
". $ \ hphantom {\ mathrm {Pr} (. 5 \ le m \ le125)} \\ approx% .3f $ "
% (m1, m2, m1, m2, quad (p, m1, m2) [0]))
plt.legend (bbox_to_anchor = (1, 1), loc = 'en haut à gauche')
plt.xlabel (" $ m $ $ \ mathrm {[g]} $ \ n crème glacée ")
plt.ylabel ("fonction de densité de probabilité \ n $ p_M (m) $ $ [\ mathrm {g ^ {- 1 }}] $ ")
plt.show ()
################################################ #############################
# graphique de la fonction de distribution cumulative et mise en évidence des valeurs pour m1 et m2
################################################ #############################
fig = plt.figure ()
plt.plot (m, P (m), lw = 3)
plt.hlines (P (m1), min (m), m1, couleur = 'C3')
plt.hlines (P (m2), min (m), m2, couleur = 'C3')
plt.vlines (m1, 0, P (m1), couleur = 'C3')
plt.vlines (m2, 0, P (m2), couleur = 'C3',
label = " $ \ mathrm {Pr} (% d \ le m \ le% d) = P_M (% d) - P_M (% d) $ \ n \ n "
". $ \ hphantom {\ mathrm {Pr} (. 5 \ le m \ le125)} =% .3f -% .3f $ \ n \ n"
". $ \ hphantom {\ mathrm {Pr} (. 5 \ le m \ le125)} \\ approx% .3f $ "
% (m1, m2, m1, m2, P (m2), P (m1), P (m2) - P (m1)))
plt.legend (bbox_to_anchor = (1, 1), loc = 'en haut à gauche')
plt.xlabel (" $ m $ $ \ mathrm {[g]} $ \ n crème glacée ")
plt.ylabel ("fonction de distribution cumulative \ n $ P_M (m) $ ")
plt.show ()