C'est ce qu'on appelle la moyenne tronquée. Fondamentalement, ce que vous faites est de calculer la moyenne des 80% du milieu de vos données, en ignorant les 10% supérieurs et inférieurs. Bien sûr, ces chiffres peuvent varier, mais c'est l'idée générale.

Une approche statistiquement raisonnable consiste à utiliser un seuil de écart-type.

Par exemple, supprimez tous les résultats de +/- 3 écarts-types.

Utiliser une règle comme «les 10% les plus gros» n'a pas de sens. Et s'il n'y a pas de valeurs aberrantes? La règle des 10% éliminerait de toute façon certaines données. Inacceptable.

Un autre test standard pour identifier les valeurs aberrantes consiste à utiliser LQ $ - $ (1,5 $ \ fois $ IQR) et UQ $ + $ (1,5 $ \ fois $ IQR). C'est un peu plus facile que de calculer l'écart type et plus général car cela ne fait aucune hypothèse sur le fait que les données sous-jacentes proviennent d'une distribution normale.

La «moyenne» dont vous parlez s'appelle en fait la «moyenne».

Elle ne répond pas exactement à votre question, mais une statistique différente qui n'est pas affectée par les valeurs aberrantes est la médiane, c'est , le nombre du milieu.

  {90,89,92,91,5} signifie: 73,4 {90,89,92,91,5} médiane: 90   pré > 
 Cela pourrait vous être utile, je ne sais pas. 

Pour un nom très spécifique, vous devrez spécifier le mécanisme de rejet des valeurs aberrantes. Un terme général est «robuste».

dsimcha mentionne une approche: le rognage. Un autre est l'écrêtage: toutes les valeurs en dehors d'une plage de valeur connue sont ignorées.

Il n'y a pas de nom officiel à cause des divers mécanismes, tels que le test Q, utilisés pour se débarrasser des valeurs aberrantes.

La suppression des valeurs aberrantes s'appelle rognage.

Aucun programme que j'ai jamais utilisé n'a average () avec un trim intégré ()

Je ne sais pas s'il a un nom, mais vous pouvez facilement trouver un certain nombre d'algorithmes pour rejeter les valeurs aberrantes:

1. Trouvez tous les nombres entre le 10e et le 90e centiles (faites-le en triant puis en rejetant les premiers $ N / 10 $ et les derniers $ N / 10 $) et prenez la valeur moyenne des valeurs restantes.

2. Trier les valeurs , rejetez les valeurs hautes et basses tant que, ce faisant, la moyenne / l'écart type change de plus de $ X \% $.

3. Trier les valeurs, rejeter les valeurs hautes et basses comme tant que ce faisant, les valeurs en question sont plus de $ K $ d'écart-type par rapport à la moyenne.

La façon la plus courante d'avoir une moyenne Robuste (le mot habituel signifiant résistant aux mauvaises données) est d'utiliser la médiane . Ce n'est que la valeur du milieu dans la liste triée (à mi-chemin entre les deux valeurs du milieu), donc pour votre exemple, ce serait 90,5 = mi-chemin entre 90 et 91.

Si vous voulez vraiment dans des statistiques robustes (telles que des estimations robustes de l'écart type, etc.) Je recommanderais de perdre le code au groupe AGORAS, mais cela peut être trop avancé pour vos besoins.

... {90,89,92,91 (, 5)} avg = 90,5

Comment décrivez-vous cette moyenne dans les statistiques? ...

Il n'y a pas de désignation spéciale pour cette méthode. Appelez-le comme vous le souhaitez, à condition que vous disiez toujours au public comment vous êtes arrivé à votre résultat, et que vous ayez les valeurs aberrantes en main pour leur montrer s'ils le demandent (et croyez-moi: ils le demanderont).

Si tout ce que vous avez est une variable (comme vous l'impliquez), je pense que certains des répondants ci-dessus sont trop critiques à l'égard de votre approche. Il est certain que d'autres méthodes qui examinent des choses comme l'effet de levier sont plus solides d'un point de vue statistique; cependant, cela implique que vous effectuez une modélisation quelconque. Si vous avez juste par exemple des scores à un test ou l'âge des seniors (cas plausibles de votre exemple), je pense qu'il est pratique et raisonnable de se méfier de la valeur aberrante que vous évoquez. Vous pouvez regarder la moyenne globale et la moyenne tronquée et voir à quel point elle change, mais cela dépendra de la taille de votre échantillon et de l'écart par rapport à la moyenne pour vos valeurs aberrantes.

Avec des valeurs aberrantes comme celles-ci, vous voudrez certainement examiner le processus de génération de données pour comprendre pourquoi c'est le cas. Est-ce une saisie de données ou un coup de chance administratif? Si tel est le cas et que cela n'a probablement aucun rapport avec la valeur réelle réelle (qui n'est pas observée), il me semble parfaitement correct de le couper. S'il s'agit d'une valeur vraie pour autant que vous puissiez le dire, vous ne pourrez peut-être pas la supprimer à moins que vous ne soyez explicite dans votre analyse à ce sujet.

J'adore la discussion ici - la moyenne tronquée est un outil puissant pour obtenir une estimation de tendance centrale concentrée au milieu des données.

La seule chose que j'ajouterais est qu'il y a un choix à faire sur la "métrique" à utiliser dans les cas de petites et grandes tailles d'échantillon. Dans certains cas, nous parlons de

• signifie dans le contexte de grands échantillons en raison du théorème de la limite centrale,
• Les médianes en tant qu'alternatives robustes pour petits échantillons
• et coupé signifie aussi robuste aux valeurs aberrantes.

De toute évidence, ce qui précède est une généralisation grossière, mais il existe des articles intéressants qui parlent des familles et des classes d'estimateurs dans les grands et petits échantillons et leurs propriétés. Je travaille en bioinformatique et généralement vous traitez avec de petits échantillons (3-10) généralement dans des modèles de souris, et ce qui ne l'est pas, et cet article donne un bon aperçu technique des alternatives existantes et des propriétés de ces estimateurs.

Restimation robuste dans de très petits échantillons

• Référence: Rousseeuw, P. J., & Verboven, S. (2002). Estimation robuste sur de très petits échantillons. Statistiques computationnelles Analyse des données &, 40 (4), 741-758.
• Lien: https://www.sciencedirect.com/science/article/pii/S0167947302000786

Il s'agit d'un article hors cours, mais il y en a beaucoup d'autres qui traitent de ces types d'estimateurs. J'espère que cela t'aides.

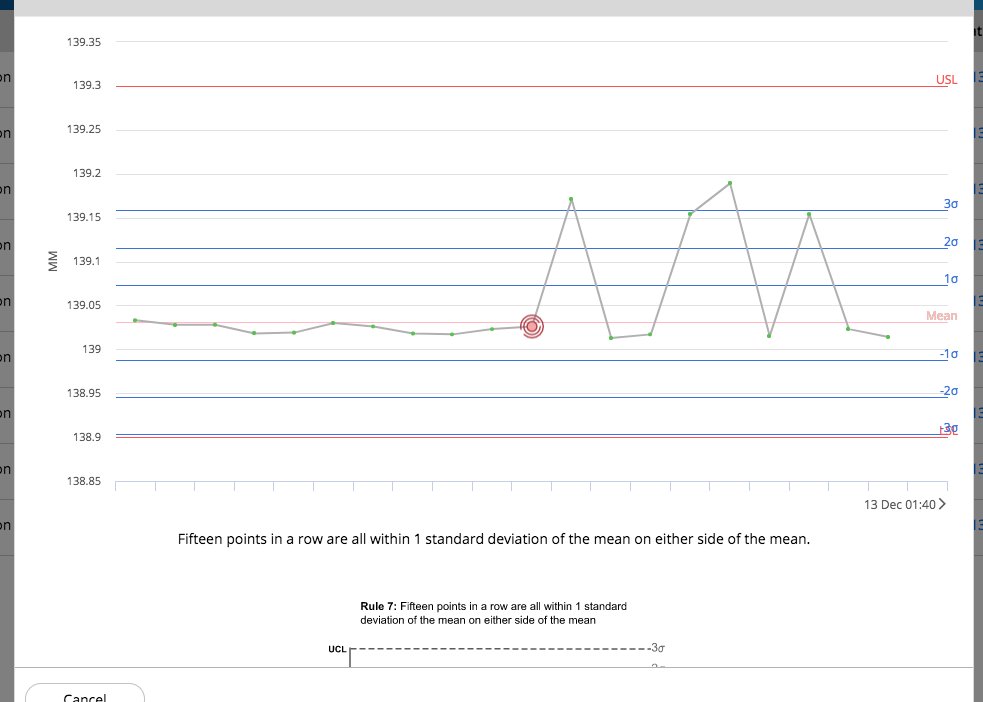
avertissement - cette méthode est ad hoc et sans étude rigoureuse. Utilisez à vos risques et périls :)

Ce que j'ai trouvé assez bon, c'est de réduire la pertinence d'une contribution en points à la moyenne par l'square de son nombre d'écarts-types par rapport à la moyenne mais seulement si le point est plus d'un écart-type de la moyenne.

Étapes:

1. Calculez la moyenne et l'écart type comme d'habitude.
2. Recalculez la moyenne, mais cette fois, pour chaque valeur, si elle est plus d'un écart-type de la moyenne réduit sa contribution à la moyenne. Pour réduire sa contribution, divisez sa valeur par le carré de son nombre d'écarts avant d'ajouter au total. De plus, parce qu'il contribue moins, nous devons réduire N, donc soustraire 1-1 / (carré de l'écart des valeurs) de N.
3. Recalculez l'écart type, mais utilisez cette nouvelle moyenne plutôt que l'ancienne.

exemple: stddev = 0,5 moyenne = 10 valeur = 11

alors, écarts = distance de la moyenne / stddev = | 10-11 | /0.5 = 2

donc la valeur passe de 11 à 11 / (2) ^ 2 = 11/4

également N change, il est réduit à N-3/4.

code:

  par défaut moyenne (données):
    "" "Renvoie l'exemple de moyenne arithmétique des données." ""
    n = len (données)
    si n < 1:
        lever ValueError ('mean requiert au moins un point de données')
    return 1.0 * sum (data) / n # en Python 2 utiliser sum (data) / float (n)

def _ss (données):
    "" "Renvoie la somme des écarts carrés des données de séquence." ""
    c = moyenne (données)
    ss = somme ((x-c) ** 2 pour x dans les données)
    retour ss, c

def stddev (données, ddof = 0):
    "" "Calcule l'écart type de la population
    par défaut; spécifiez ddof = 1 pour calculer l'échantillon
    écart-type."""
    n = len (données)
    si n < 2:
        lever ValueError ('la variance nécessite au moins deux points de données')
    ss, c = _ss (données)
    pvar = ss / (n-ddof)
    retourne pvar ** 0,5, c

def rob_adjusted_mean (valeurs, s, m):
    n = 0,0
    tot = 0,0
    pour v en valeurs:
        diff = abs (v - m)
écarts = diff / s
        si écarts > 1:
            # c'est une valeur aberrante, alors réduisez sa pertinence / pondération par carré de son nombre d'écarts
            n + = 1,0 / écarts ** 2
            tot + = v / écarts ** 2
        autre:
            n + = 1
            tot + = v
    retour tot / n

def rob_adjusted_ss (valeurs, s, m):
    "" "Renvoie la somme des écarts carrés des données de séquence." ""
    c = rob_adjusted_mean (valeurs, s, m)
    ss = somme ((x-c) ** 2 pour x en valeurs)
    retour ss, c

def rob_adjusted_stddev (données, s, m, ddof = 0):
    "" "Calcule l'écart type de la population
    par défaut; spécifiez ddof = 1 pour calculer l'échantillon
    écart-type."""
    n = len (données)
    si n < 2:
        lever ValueError ('la variance nécessite au moins deux points de données')
    ss, c = rob_adjusted_ss (données, s, m)
    pvar = ss / (n-ddof)
    retourne pvar ** 0,5, c

s, m = stddev (valeurs, ddof = 1)
imprimer s, m
s, m = rob_adjusted_stddev (valeurs, s, m, ddof = 1)
imprimer s, m
 

sortie avant et après ajustement de mes 50 mesures:

  0.0409789841609 139.04222
0,0425867309757 139,030745443
 

Il existe des méthodes supérieures aux méthodes basées sur IQR ou SD. En raison de la présence de valeurs aberrantes, la distribution a probablement déjà des problèmes de normalité (sauf si les valeurs éloignées sont uniformément réparties aux deux extrémités de la distribution). Cela gonfle beaucoup le SD, ce qui rend l'utilisation des SD moins que souhaitable, mais la méthode SD présente certains aspects souhaitables par rapport à la méthode IQR, à savoir que 1,5 fois le IQR est un seuil relativement subjectif. Si la subjectivité dans ces domaines est inévitable, il est préférable de la réduire.

Un identificateur Hampel, quant à lui, utilise des méthodes robustes pour estimer les valeurs aberrantes. Essentiellement, c'est la même chose que la méthode SD, mais vous remplaceriez les moyennes par des médianes et SD par des écarts absolus médians (MAD). Les MAD ne sont que la distance médiane des médias. Ce MAD est multiplié par une constante de mise à l'échelle .675. La formule sort à (X - Médiane) / (. 675 * MAD). La statistique résultante est traitée de manière identique à un score Z. Cela contourne le problème de la non-normalité probable que si vous avez des valeurs aberrantes peuvent être présentes.

Quant à savoir comment l'appeler. Les moyens découpés sont normalement réservés à la méthode de découpage des dix pour cent inférieurs et supérieurs mentionnés par @dsimcha. S'il a été complètement nettoyé, vous pouvez vous y référer comme moyen de nettoyage ou simplement comme moyen. Assurez-vous simplement d'être clair ce que vous en avez fait dans votre article.

Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., & Stahel, W. A. ​​(1986). Statistiques robustes. John Wiley & Sons, New York.

Cela peut être la médiane. Pas toujours, mais parfois. Je n'ai aucune idée de comment cela s'appelle à d'autres occasions. J'espère que cela a aidé. (Au moins un peu.)

Mon manuel de statistiques se réfère à cela comme une moyenne d'échantillon par opposition à une moyenne de population. L'échantillon implique qu'une restriction a été appliquée à l'ensemble de données complet, même si aucune modification (suppression) n'a été apportée à l'ensemble de données.