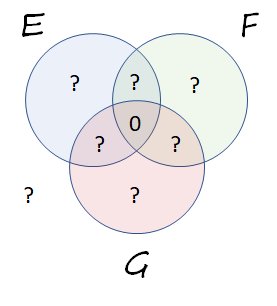
TCe diagramme de Venn affiche une situation où la chance d'intersection mutuelle est nulle:

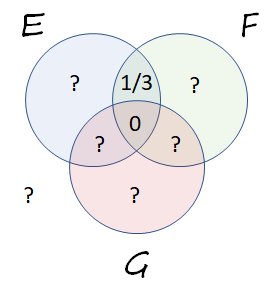
From $ \ Pr (E \ cap F) = 1/3 $ nous en déduisons toute cette probabilité réside dans le chevauchement des $ E $ et $ F $ disques, mais pas dans le chevauchement mutuel des trois disques. Cela nous permet de mettre à jour le diagramme:

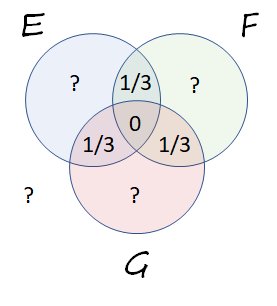
En appliquant le même raisonnement à $ \ Pr (F \ cap G) = \ Pr (E \ cap G) = 1/3, $ nous obtenons un Venn diagramme affichant toutes les informations de la question:

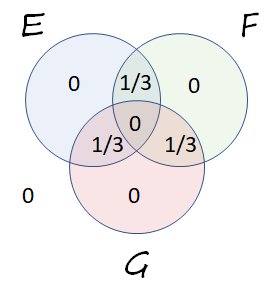
L ' Axiome de probabilité totale affirme la somme de toutes les probabilités (y compris la probabilité pour le complément de $ E \ cup F \ cup G, $ affiché en bas à gauche) est $ 1. $

Un axiome de probabilité encore plus basique affirme que toutes les probabilités doivent être non négatives. Mais puisque $ 1/3 + 1/3 + 1/3 + 0 = 1, $ toutes les probabilités possibles apparaissent déjà. Les probabilités restantes doit être zéro, ce qui signifie L'image ne peut être complétée que comme ceci:

Enfin, un troisième axiome (le même que celui utilisé dans la deuxième étape de remplissage du diagramme de Venn) affirme la probabilité que $ E $ soit égal à la somme des probabilités de ses quatre parties, car elles sont disjointes. Ainsi, en commençant par la probabilité centrale et en se déplaçant dans le sens antihoraire autour du disque qui représente $ E, $ span >

$$ \ Pr (E) = 0 + 1/3 + 0 + 1/3 = 2/3. $$

One morale à retenir:

Tracez des diagrammes de Venn en toute généralité afin qu'ils montrent toutes les intersections possibles des ensembles, même lorsque vous savez que certaines probabilités sont nulles.

Cela vous aide à garder une trace de toutes les informations systématiquement.(C'est aussi conceptuellement plus précis, car les ensembles de probabilité nulle ne doivent pas nécessairement être non vides!)

Si vous essayez de remplir le diagramme de Venn, vous ne pouvez pas placer d'entrées non nulles dans des régions autres que celles représentées par des intersections par paires.Ils formeront l'espace échantillon par eux-mêmes, ce qui signifie $$ \ mathbb P (E) = \ mathbb P (E \ cap F) + \ mathbb P (E \ cap G) = 2/3 $$

La réponse à la question "Pouvez-vous déterminer $ P (E) $ ?" est Yes.

Étant donné les événements $ E, F, G $ définis sur un exemple d'espace $ \ Omega $ , nous savons que \ begin {align} &E \ cap F \ cap G \\ &E \ cap F \ cap G ^ c \\ &E \ cap F ^ c \ cap G \\ &E \ cap F ^ c \ cap G ^ c \\ &E ^ c \ cap F \ cap G \\ &E ^ c \ cap F \ cap G ^ c \\ &E ^ c \ cap F ^ c \ cap G \\ &E ^ c \ cap F ^ c \ cap G ^ c \\ \ end {align} sont des événements $ 8 $ s'excluant mutuellement dont l'union est $ \ Omega $ . Ainsi, la somme des probabilités de ces événements 8 $ est 1 $ . Maintenant, on nous dit que $ E, F, G $ ne peut pas se produire simultanément, c'est-à-dire $ E \ cap F \ cap G = \ emptyset $ et ainsi $ P (E \ cap F \ cap G) = 0 $ . On nous dit aussi que \ begin {align} P (E \ cap F) & = P (E \ cap F \ cap G) + P (E \ cap F \ cap G ^ c) = \ frac 13 \\ P (E \ cap G) & = P (E \ cap F \ cap G) + P (E \ cap F ^ c \ cap G) = \ frac 13 \\ P (F \ cap G) & = P (E \ cap F \ cap G) + P (E ^ c \ cap F \ cap G) = \ frac 13 \ end {align} où nous pouvons nous sentir à l'aise sur la somme au milieu de chaque équation en réfléchissant au fait que la probabilité de l ' union de deux événements mutuellement exclusifs est la somme des probabilités des deux événements. Puisque $ P (E \ cap F \ cap G) = 0 $ , nous concluons que \ begin {align} P (E \ cap F) & = P (E \ cap F \ cap G ^ c) = \ frac 13 \\ P (E \ cap G) & = P (E \ cap F ^ c \ cap G) = \ frac 13 \\ P (F \ cap G) & = P (E ^ c \ cap F \ cap G) = \ frac 13 \ end {align}

Mais, parmi les $ 8 $ événements mutuellement exclusifs répertoriés ci-dessus dont l'union est $ \ Omega $ ,nous avons identifié trois événements dont les probabilités s'élèvent à $ 1 $ et donc les autres événements $ 5 $ (l'un desqui est $ E \ cap F \ cap G $ ) doit avoir une probabilité $ 0 $ .Par conséquent, \ begin {align} P (E) & = P (E \ cap F \ cap G) + P (E \ cap F \ cap G ^ c) + P (E \ capF ^ c \ cap G) + P (E \ cap F ^ c \ cap G ^ c) \\ & = 0 + \ frac 13 + \ frac 13 + 0 \\ & = \ frac 23 \ end {align} Par symétrie (ou par une répétition par force brute des arguments ci-dessus mutatis mutandis ), nous pouvons conclure que $ E, F, G $ tous ont la probabilité $ \ frac 23 $ .

Pouvons-nous y penser de cette façon?

P (E ∩ F) = P (F ∩ G) = P (E ∩ G) = 1/3

P (E ∩ F) + P (F ∩ G) + P (E ∩ G) = 1

Ce qui signifie que la probabilité que l'événement E se produise par lui-même est nulle, ce qui signifie qu'il ne peut se produire qu'avec F ou G et qu'il ne peut pas se produire avec les deux.

P (E) = P (E ∩ F) + P (E ∩ G) = 1/3 + 1/3 = 2/3

Depuis les événements $ (E, F) $ , $ (E, G) $ $ (F, G) $ sont mutuellement exclusifs et additionnés à un, nous pouvons utiliser la loi du prob total: $$ P (E) = P (E, F) + P (E, G) = \ tfrac {2} {3} $$ Puisque $ P (E \ mid E, F) P (E, F) = P (E, F) $ , idem pour $ E, G $ et $ P (E \ mid F, G) = 0 $ .