J'aime les images illustrant comment différents modèles peuvent avoir une corrélation similaire.Ceux ci-dessous sont issus d'articles de Wikipédia sur la corrélation et la dépendance

et le quatuor d'Anscombe avec des corrélations d'environ 0,816 $

Le paradoxe de Simpson

Un phénomène qui apparaît lorsqu'une variable clé est omise de l'analyse d'une relation entre une ou plusieurs variables indépendantes et une variable dépendante.Par exemple, cela montre que plus les maisons ont de chambres, plus le prix de la maison est bas :

qui semble contre-intuitif, et se résout facilement en traçant tous les points de données qui composent la moyenne pour chaque zone, sur le même graphique.Ici, le plus grand nombre de chambres indique correctement les maisons les plus chères en observant également la variable quartier:

Si vous souhaitez en savoir plus sur l'exemple ci-dessus et obtenir une bien meilleure explication que celle que j'ai pu fournir, cliquez ici.

L'un des concepts les plus intéressants qui sont aujourd'hui très importants et très faciles à visualiser est "overfitting".Le classificateur vert ci-dessous présente un exemple clair de surajustement [Edit: "le classificateur vert est donné par la ligne très ondulée séparant les points de données rouges et bleus" - Nick Cox].

De Wikipédia:

Comment fonctionne un jeu de données 2D où la moyenne de X est de 54 avec un SD 17, et pour Y 48 et 27, respectivement, et la corrélation entre les deux est de -0,06?

Présentation de l ' Anscombosaurus:

Et son compagnon, le Datasaurus Dozen:

Je pense que les fausses corrélations méritent également leur propre message.C'est à dire.la corrélation n'égale pas la causalité.Peut-être l'une des choses les plus souvent utilisées pour tenter de contourner la vérité à l'aide de statistiques.Tyler Vigen a un site Web célèbre avec de nombreux exemples.Pour illustrer, voyez le graphique ci-dessous où le nombre de cas de polio et les ventes de crème glacée sont clairement corrélés.Mais supposer que la polio entraîne des ventes de crème glacée ou l'inverse est clairement absurde.

P.S: xkcd 1 pertinent et xkcd 2 pertinent

Le biais peut être bon

Un $ \ color {orangered} {\ text {estimateur sans biais}} $ est en moyenne correct. Un $ \ color {steelblue} {\ text {biased estimator}} $ est en moyenne incorrect.

Pourquoi alors voudriez-vous utiliser un estimateur biaisé (par exemple, la régression des crêtes)?

La réponse est que introduire un biais peut réduire la variance.

Dans l'image, pour un échantillon donné, le $ \ color {orangered} {\ text {estimateur sans biais}} $ , a un 68 $ \% $ chance d'être dans $ 1 $ unité arbitraire du paramètre vrai, tandis que le $ \ color {steelblue} {\ text {biased estimator}} $ a une chance beaucoup plus grande de $ 84 \% $ .

Si le biais que vous avez introduit réduit suffisamment la variance de l'estimateur, votre seul échantillon a de meilleures chances de produire une estimation proche du paramètre de population.

"En moyenne correct" sonne bien, mais ne donne aucune garantie sur la mesure dans laquelle les estimations individuelles peuvent s'écarter du paramètre de population. Si vous dessinez de nombreux échantillons, le $ \ color {steelblue} {\ text {biaisé estimator}} $ serait en moyenne erroné par 0,5 $ unités arbitraires. Cependant, nous avons rarement beaucoup d'échantillons de la même population pour observer cette «estimation moyenne», nous préférerions donc avoir de bonnes chances d'être proches du vrai paramètre.

Lors de la première compréhension des estimateurs et de leur erreur, il est utile de comprendre deux sources d'erreur: le biais et la variance.L'image ci-dessous illustre parfaitement cela tout en mettant en évidence les compromis entre ces deux sources d'erreur.

La bulle est la vraie valeur que l'estimateur tente d'estimer et chaque point représente une estimation de cette valeur.Idéalement, vous avez un biais et une variance faibles, mais les autres fléchettes représentent des estimateurs moins qu'idéaux.

PAnalyse des composants principaux (PCA) PCA est une méthode de réduction de dimension.Il projette les variables d'origine dans la direction qui maximise la variance.

Dans notre figure, les points rouges proviennent d'une distribution normale bivariée.Les vecteurs sont les vecteurs propres et la taille de ces vecteurs est proportionnelle aux valeurs des valeurs propres respectives.L'analyse en composantes principales fournit de nouvelles directions orthogonales et pointant vers les directions de forte variance.

Vecteurs propres & Valeurs propres

Le concept de vecteurs propres et de valeurs propres qui sont à la base de l'analyse en composantes principales (ACP), comme expliqué sur wikipedia:

En substance, un vecteur propre $ v $ d'une transformation linéaire $ T $ est un vecteur différent de zéro qui, lorsque $ T $ lui est appliqué, ne change pas de direction. L'application de $ T $ au vecteur propre ne met à l'échelle le vecteur propre que par la valeur scalaire $ \ lambda $ , appelée un valeur propre. Cette condition peut être écrite comme l'équation: $ T (v) = \ lambda v $ .

La déclaration ci-dessus est très élégamment expliquée en utilisant ce gif:

Vecteurs indiqués en bleu $ \ begin {bmatrix} 1 \\ 1 \\ \ end {bmatrix} $ et magenta $ \ begin {bmatrix} 1 \\ - 1 \\ \ end {bmatrix} $ sont des vecteurs propres pour la transformation linéaire, $ T = \ begin {bmatrix} 2 & 1 \\ 1 & 2 \\ \ end {bmatrix} $ . Les points qui se trouvent sur la ligne passant par l'origine, parallèles aux vecteurs propres, restent sur la ligne après la transformation. Les vecteurs en rouge ne sont pas des vecteurs propres, donc leur direction est modifiée par la transformation. Les vecteurs bleus sont mis à l'échelle d'un facteur 3 - qui est la valeur propre du vecteur propre bleu, tandis que les vecteurs magenta ne sont pas mis à l'échelle, car leur valeur propre est 1.

Lien vers l'article Wikipedia.

Tvariance du biais de compromis est un autre concept très important dans les statistiques / apprentissage automatique.

Les points de données en bleu proviennent de $ y (x) = \ sin (x) + \ epsilon $ , où $ \ epsilon $ a une distribution normale. Les courbes rouges sont estimées à l'aide de différents échantillons. La figure «Large Variance and Small Bias» présente le modèle original, qui est un réseau de fonctions de base radiale avec 24 bases gaussiennes.

La figure "Small Variance and Large Bias" présente le même modèle régularisé.

Notez que dans la figure "Petite variance et grand biais" les courbes rouges sont très proches les unes des autres (petite variance). La même chose ne se produit pas dans la figure "Grande variance et petit biais" (grande variance).

Spetite variance et grand biais

Large variance et petit biais

De mon cours de méthodes informatiques et d'apprentissage automatique.

En voici une très basique, mais à mon avis très puissante car ce n'est pas seulement une explication visuelle d'un concept mais demande également de visualiser ou d'imaginer un objet réel représentant le concept:

Les néophytes ont parfois du mal à comprendre des concepts très basiques comme la moyenne, la médiane et le mode.

Donc, pour les aider à mieux saisir l'idée de méchanceté:

Prenez cette distribution biaisée et faites-en une impression 3D, en plastique, ou sculptez-la dans du bois, vous avez maintenant un véritable objet entre vos mains.Essayez de l'équilibrer en utilisant un seul doigt ... la moyenne est le point only où vous pouvez le faire.

La figure ci-dessous montre l'importance de définir précisément les objectifs et les hypothèses d'un problème de clustering (et d'un problème statistique général).Différents modèles peuvent donner des résultats très différents:

Sources: ScikitLearn

D'accord, donc celui-ci est moins une illustration d'un concept de base, mais il est très intéressant à la fois visuellement et en termes d'applications. Je pense que montrer aux gens ce qu'ils peuvent finalement accomplir avec ce qu'ils apprennent est une excellente forme de motivation, vous pouvez donc le présenter comme un exemple de développement et d'application de modèles statistiques, qui dépend de tous les concepts statistiques plus fondamentaux qu'ils apprennent. Sur ce, je vous présente ...

Species Distribution Modelling

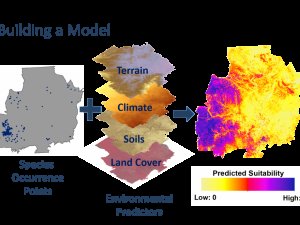
C'est en fait un sujet très large avec beaucoup de nuances en termes de types de données, de collecte de données, de configuration de modèle, d'hypothèses, d'applications, d'interprétations, etc. Mais en termes simples, vous prenez des exemples d'informations sur l'emplacement d'une espèce, puis utiliser ces emplacements pour échantillonner des variables environnementales potentiellement pertinentes (par exemple, données climatiques, données sur le sol, données sur l'habitat, altitude, pollution lumineuse, pollution sonore, etc.), développer un modèle en utilisant les données (par exemple, GLM, modèle de processus ponctuel, etc.) , puis utilisez ce modèle pour prédire dans un paysage à l'aide de vos variables environnementales. En fonction de la configuration du modèle, ce qui est prédit peut être un habitat convenable potentiel, des zones d'occurrence probables, la distribution des espèces, etc. Vous pouvez également modifier les variables environnementales pour voir comment elles affectent ces résultats. Les gens ont utilisé des MDS pour trouver des populations auparavant inconnues d'une espèce, ils les ont utilisés pour découvrir de nouvelles espèces, avec des données climatiques historiques, ils les ont utilisées pour prédire à rebours dans le temps où une espèce se trouvait et comment elle est arrivée là où elle est aujourd'hui (même tout au long des périodes de glaciation), et avec des choses comme les prévisions climatiques futures et la perte d'habitat, elles sont utilisées pour prédire comment les activités humaines affecteront l'espèce à l'avenir. Ce ne sont là que quelques exemples, et si j'ai le temps plus tard, je trouverai et relierai des articles intéressants. En attendant, voici une petite image que j'ai trouvée illustrant les bases: