L'affaire Krasnodar Krai n'est pas la seule. Vous trouverez ci-dessous un graphique pour les données de 36 régions (j'ai sélectionné les meilleurs exemples sur 84) où nous voyons soit
- une sous-dispersion similaire
- ou du moins les nombres semblent atteindre un plateau autour d'un "joli" nombre (j'ai tracé des lignes à 10, 25, 50 et 100, là où plusieurs régions trouvent leur plateau)

À propos de l'échelle de ce graphique: cela ressemble à une échelle logarithmique pour l'axe des y, mais ce n'est pas le cas. C'est une échelle de racine carrée. J'ai fait cela de telle sorte qu'une dispersion comme pour les données distribuées de Poisson $ \ sigma ^ 2 = \ mu $ aura la même apparence pour tous les moyens. Voir aussi: Pourquoi la transformation de racine carrée est-elle recommandée pour les données de comptage?
Ces données recherchent certains cas clairement sous-dispersés, s'il s'agissait d'une distribution de Poisson. (Whuber a montré comment dériver une valeur de signification, mais je suppose que cela passe déjà le test de traumatisme interoculaire. J'ai quand même partagé cette intrigue parce que j'ai trouvé intéressant qu'il y ait des cas sans sous-dispersion, mais ils semblent néanmoins coller à un plateau. Il peut y avoir plus qu'une simple sous-dispersion. Ou il y a des cas comme le n ° 15 et le n ° 22, en bas à gauche de l'image, qui montrent une sous-dispersion, mais pas la valeur de plateau fixe.).
La sous-dispersion est en effet étrange. Mais nous ne savons pas quel type de processus a généré ces chiffres. Ce n'est probablement pas un processus naturel et des humains sont impliqués. Pour une raison quelconque, il semble qu'il y ait un certain plateau ou une limite supérieure. Nous ne pouvons que deviner ce que cela pourrait être (ces données ne nous en disent pas grand chose et il est hautement spéculatif de l'utiliser pour deviner ce qui pourrait se passer). Il peut s'agir de données falsifiées, mais il peut également s'agir d'un processus complexe qui génère les données et a une limite supérieure (par exemple, ces données sont des cas signalés / enregistrés et peut-être le signalement / enregistrement est limité à un nombre fixe).
### à l'aide du fichier JSON suivant
### https://github.com/mediazona/data-corona-Russia/blob/master/data.json
bibliothèque (rjson)
#data <- fromJSON (fichier = "~ / Downloads / data.json")
données <- fromJSON (file = "https://raw.githubusercontent.com/mediazona/data-corona-Russia/master/data.json")
layout (matrice (1: 36,4, byrow = TRUE))
par (mar = c (3,3,1,1), mgp = c (1,5,0,5,0))
## moyens de calcul et dispersion des 9 derniers jours
signifie <- rep (0,84)
disp <- rep (0,84)
pour (i en 1:84) {
x <- c (-4: 4)
y <- data [[2]] [[i]] $ confirmé [73:81]
signifie [i] <- mean (y)
mod <- glm (y ~ x + I (x ^ 2) + I (x ^ 3), famille = poisson (lien = identité), start = c (2,0,0,0))
disp [i] <- mod $ deviance / mod $ df.residual
}
### choisir des étuis intéressants et les commander
cas <- c (4,5,11,12,14,15,21,22,23,24,
26,29,30,31,34,35,37,41,
42,43,47,48,50,51,53,56,
58,67,68,71,72,75,77,79,82,83)
cases <- cases [ordre (signifie [cases])]
pour (i dans les cas) {
col = 1
si (i == 24) {
col = 2
bg = "rouge"
}
plot (-100, -100, xlim = c (0,85), ylim = c (0,11), yaxt = "n", xaxt = "n",
xlab = "", ylab = "compte", col = col)
axis (2, at = c (1:10), labels = c (1:10) ^ 2, las = 2)
axis (1, at = c (1:85), labels = rep ("", 85), tck = -0.04)
axis (1, at = c (1,1 + 31,1 + 31 + 30) -1, labels = c ("Mar 1", "Apr 1", "May 1"), tck = -0.08)
pour (lev dans c (10,25,50,100)) {
#polygon (c (-10,200,200, -10), sqrt (c (lev-sqrt (lev), lev-sqrt (lev), lev + sqrt (lev), lev + sqrt (lev))),
# col = "gris")
lignes (c (-10200), sqrt (c (lev, lev)), lty = 2)
}
lignes (sqrt (data [[2]] [[i]] $ confirmé), col = col)
points (sqrt (données [[2]] [[i]] $ confirmées), bg = "white", col = col, pch = 21, cex = 0.7)
title (paste0 (i, ":", data [[2]] [[i]] $ name), cex.main = 1, col.main = col)
}
### un graphique intéressant de sous / surdispersion et de la moyenne des 9 derniers points de données
### on peut reconnaître un cluster avec une faible déviance et signifie juste en dessous de 100
plot (signifie, disp, log = "xy",
yaxt = "n", xaxt = "n")
axe (1, las = 1, tck = -0.01, cex.axis = 1,
at = c (100 * c (1: 9), 10 * c (1: 9), 1 * c (1: 9)), labels = rep ("", 27))
axe (1, las = 1, tck = -0.02, cex.axis = 1,
étiquettes = c (1,10,100,1000), à = c (1,10,100,1000))
axe (2, las = 1, tck = -0.01, cex.axis = 1,
at = c (10 * c (1: 9), 1 * c (1: 9), 0.1 * c (1: 9)), labels = rep ("", 27))
axe (2, las = 1, tck = -0.02, cex.axis = 1,
étiquettes = c (1,10,100,1000) / 10, à = c (1,10,100,1000) / 10)
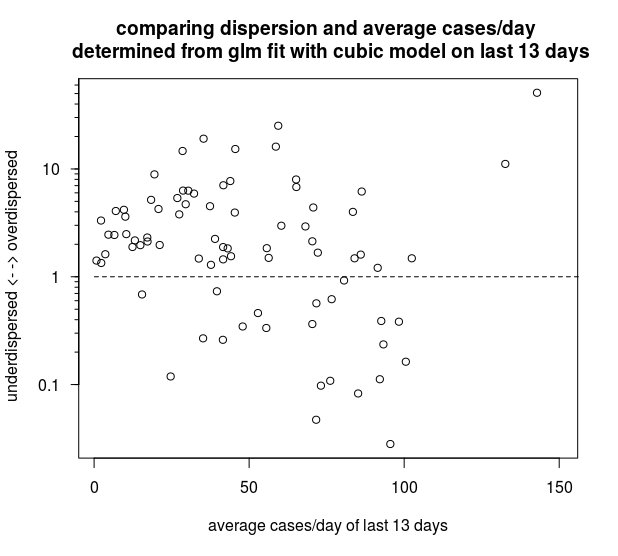
Peut-être que cela surinterprète un peu les données, mais de toute façon voici un autre graphique intéressant (également dans le code ci-dessus). Le graphique ci-dessous compare les 84 régions (à l'exception des trois plus grandes qui ne rentrent pas dans le graphique) en fonction de la valeur moyenne des 13 derniers jours et d'un facteur de dispersion basé sur un modèle GLM avec la famille de Poisson et un ajustement cubique. Il semble que les cas de sous-dispersion sont souvent proches de 100 cas par jour.
Il semble que quelle que soit la cause de ces valeurs de niveau suspect dans le kraï de Krasnodar, cela se produit dans plusieurs régions, et cela pourrait être lié à une limite de 100 cas / jour. Il est possible qu'une censure se produise dans le processus qui génère les données et qui limite les valeurs à une limite supérieure. Quel que soit ce processus qui cause les données censurées, il semble se produire dans plusieurs régions de la même manière et a probablement une cause artificielle (humaine) (par exemple une sorte de limitation des tests de laboratoire dans les petites régions).