La probabilité qu'un dé ne se présente pas $ n $ est 1-1 $ / n $ .La probabilité de ne pas afficher $ n $ dans l'un des dés $ n $ est de $ (1-1 / n) ^ n $ .Si vous soustrayez cela de $ 1 $ , il y aura probabilité d'au moins un $ n $ lorsque vous lancez des dés $ n $ , c'est-à-dire

$$ p = 1- (1-1 / n) ^ n \ rightarrow 1-e ^ {- 1} $$ comme $ n $ va à $ \ infty. $

L'événement $ A: = $ "au moins un dé apparaît sur le côté $ n $ "est le complément de l'événement $ B: = $ " tous les dés tournent sur des $ n $ côtés ".

Donc $ P (A) = 1-P (B) $ . Qu'est-ce que $ P (B) $ ?

Tous les dés sont indépendants, donc

$$ P (\ text {tous les dés $ n $ tournent sur des côtés non $ n $}) = P (\ text {un seul dé donne un résultat différent de - $ n $}) ^ n = \ bigg (\ frac {n-1} {n} \ bigg) ^ n. $$

Alors

$$ P (A) = 1- \ bigg (\ frac {n-1} {n} \ bigg) ^ n. $$

Faites confiance, mais vérifiez. J'aime le faire en R:

  > nn <- 6
> n_sims <- 1e5
> sum (replicate (n_sims, any (sample (1: nn, nn, replace = TRUE) == nn))) / n_sims
[1] 0,66355
> 1 - ((nn-1) / nn) ^ nn
[1] 0,665102
 

Ça a l'air bien. Essayez ceci avec d'autres valeurs de nn . Voici un graphique:

  nn <- 2: 100
plot (nn, 1 - ((nn-1) / nn) ^ nn, type = "o", pch = 19, ylim = c (1-1 / exp (1), 1))
abline (h = 1-1 / exp (1), col = "rouge")
 

Nous notons comment notre probabilité dans la limite est

$$ P (A) = 1- \ bigg (\ frac {n-1} {n} \ bigg) ^ n = 1- \ bigg (1- \ frac {1} {n} \ bigg) ^ n \ à 1- \ frac {1} {e} \ environ 0,6321206 \ quad \ text {as} n \ à \ infty, $$

à cause d'une identité impliquant $ e $ .

Les réponses de @StephanKolassa (+1) et @gunes (+1) sont toutes les deux très bien. Mais ce problème peut être résolu en référence à binomial et Poisson distributions comme suit:

Si $ X_n $ est le nombre de n vus dans $ n $ span> jets d'un dé juste à côté de $ n $ , puis $ X_n \ sim \ mathsf {Binom} (n, 1 / n), $ pour que $ P (X_n \ge 1) = 1 - P (X_n = 0) = 1- (1-1 / n) ^ n. $

Comme $ n \ rightarrow \ infty, $ on a $ X_n \ stackrel {prob} {\ rightarrow} Y\ sim \ mathsf {Pois} (\ lambda = 1), $ avec $ P (Y \ ge 1) = 1 - P (Y = 0) = 1 -e ^ {- 1}. $

La réponse peut également être trouvée en comptant uniquement les événements décrits, bien que la réponse acceptée soit plus élégante . Nous allons considérer le cas de la filière, et j'espère que la généralisation est évidente. Nous laisserons l'espace événementiel être toutes les séquences de nombres de $ \ {1,2, ..., 6 \} $ de longueur 6 $ . En voici quelques exemples (choisis au hasard):

  3 2 3 5 6 1
1 1 2 5 2 4
1 2 1 1 6 3
4 4 3 3 4 2
6 1 1 6 3 4
6 3 5 4 5 1
 

Le fait est que notre espace a un total d'événements $ 6 ^ 6 $ , et en raison de l'indépendance, nous supposons que l'un d'entre eux est aussi probable que l'autre (uniformément distribué). Nous devons compter le nombre de séquences contenant au moins un $ 6 $ . Nous partitionnons l'espace que nous comptons en fonction du nombre de $ 6 $ qui apparaissent, alors considérez le cas où exactement un $ 6 $ apparaît. De combien de façons cela peut-il se produire? Les six peuvent apparaître dans n'importe quelle position (6 positions différentes), et quand c'est le cas, les 5 autres positions peuvent avoir l'un des 5 symboles différents (de $ \ {1,2, ... , 5 \} $ ). Alors le nombre total de séquences avec exactement un $ 6 $ est: $ \ binom {6} {1} 5 ^ 5 $ . De même pour le cas où il y a exactement deux $ 6 $ : on obtient qu'il y a exactement $ \ binom {6} {2} 5 ^ 4 $ de telles séquences. Il est maintenant temps de s'amuser avec les sommes :

$$ \ sum_ {k = 1} ^ 6 \ binom {6} {k} 5 ^ {6-k} = \ sum_ {k = 0} ^ 6 \ binom {6} {k} 5 ^ {6-k} 1 ^ k - 5 ^ 6 = (5 + 1) ^ 6 - 5 ^ 6 $$

Pour obtenir une probabilité à partir de ce décompte, nous divisons par le nombre total d'événements:

$$ \ frac {6 ^ 6 - 5 ^ 6} {6 ^ 6} = 1 - (5/6) ^ 6 = 1 - (1-1 / 6 ) ^ 6 $$

Je pense que cela se généralise assez bien, car pour tout $ n $ autre que $ 6 $ ,les mêmes arguments sont valables, remplacez chaque occurrence de $ 6 $ par $ n $ et $ 5 $ avec $ n-1 $ .

Il convient également de noter que ce nombre $ 5 ^ 6 = \ binom {6} {0} 5 ^ 6 $ est la contribution de séquences dans lesquelles aucun $ 6 $ se produit et est beaucoup plus facile à calculer (tel qu'utilisé dans la réponse acceptée).

J'ai trouvé la réponse de BruceET intéressante, relative au nombre d'événements. Une autre manière d'aborder ce problème est d'utiliser la correspondance entre le temps d'attente et le nombre d'événements. L'utilisation de cela serait que le problème pourra être généralisé d'une certaine manière plus facilement.

Affichage du problème comme un problème de temps d'attente

Cette correspondance, comme par exemple expliqué / utilisé ici et ici, est

Pour le nombre de lancers de dés $ m $ et le nombre de coups / événements $ k $ vous avoir: $$ \ begin {array} {ccc} \ overbrace {P (K \ geq k | m)} ^ {\ text {c'est ce que vous cherchez}} & = & \ overbrace {P (M \ leq m | k)} ^ {\ text {nous allons l'exprimer à la place}} \\ {\ small \ text {$ \ mathbb {P} $ $ k $ ou plus d'événements dans $ m $ lancers de dés}} & = & {\ small \ text {$ \ mathbb {P} $ jetons de dés en dessous de $ m $ donné $ k $ événements}} \ end {tableau} $$

En mots: la probabilité d'obtenir plus de $ K \ geq k $ événements (par exemple $ \ geq 1 $ fois 6) dans un certain nombre de lancers de dés $ m $ est égal à la probabilité d'avoir besoin de $ m $ ou moins de dés pour obtenir $ k $ de tels événements.

Cette approche concerne de nombreuses distributions.

  Distribution de la distribution de
Temps d'attente entre les événements nombre d'événements

Poisson exponentiel
Erlang / Gamma sur / sous-dispersé Poisson
Binôme géométrique
Binomial négatif sur / sous-dispersé Binomial
 

Donc, dans notre situation, le temps d'attente est une distribution géométrique. La probabilité que le nombre de dés lancés $ M $ avant de lancer le premier $ n $ soit inférieure à ou égal à $ m $ (et étant donné une probabilité de rouler $ n $ est égal à $ 1 / n $ ) est le CDF suivant pour la distribution géométrique:

$$ P (M \ leq m) = 1- \ left (1- \ frac {1} {n} \ right) ^ m $$

et nous recherchons la situation $ m = n $ donc vous obtenez:

$$ P (\ text {il y aura un $ n $ roulé dans $ n $ rolls}) = P (M \ leq n) = 1- \ left (1 - \ frac {1} {n} \ right) ^ n $$

Généralisations, lorsque $ n \ to \ infty $

La première généralisation est que pour $ n \ to \ infty $ la distribution du nombre d'événements devient Poisson avec le facteur $ \ lambda $ et le temps d'attente devient une distribution exponentielle avec le facteur $ \ lambda $ . Ainsi, le temps d'attente pour lancer un événement dans le processus de lancement des dés de Poisson devient $ (1-e ^ {- \ lambda \ times t}) $ et avec $ t = 1 $ nous obtenons le même résultat $ \ environ 0,632 $ que les autres réponses. Cette généralisation n'est pas encore si particulière car elle ne reproduit que les autres résultats, mais pour le suivant je ne vois pas aussi directement comment la généralisation pourrait fonctionner sans penser aux temps d'attente.

Généralisations, quand les dés ne sont pas justes

Vous pourriez envisager la situation où les dés ne sont pas justes. Par exemple, une fois, vous lancerez un dé avec une probabilité de 0,17 de lancer un 6, et une autre fois, vous lancerez un dé avec une probabilité de 0,16 de lancer un 6. Cela signifiera que les 6 seront plus regroupés autour des dés avec un biais positif. , et que la probabilité de lancer un 6 en 6 tours sera inférieure au chiffre 1-1 $ / e $ . (cela signifie que sur la base de la probabilité moyenne d'un seul jet, disons que vous l'avez déterminée à partir d'un échantillon de plusieurs lancers, vous ne pouvez pas déterminer la probabilité dans de nombreux lancers avec les mêmes dés, car vous devez prendre en compte la corrélation du dés)

Disons qu'un dé n'a pas de probabilité constante $ p = 1 / n $ , mais à la place il est tiré d'une distribution bêta avec une moyenne $ \ bar {p} = 1 / n $ et un paramètre de forme $ \ nu $

$$ p \ sim Beta \ left (\ alpha = \ nu \ frac {1} {n}, \ beta = \ nu \ frac {n-1} {n } \ droite) $$

Ensuite, le nombre d'événements pour un dé particulier lancé $ n $ time sera binomial bêta distribué. Et la probabilité pour 1 ou plusieurs événements sera:

$$ P (k \ geq 1) = 1 - \ frac {B (\ alpha, n + \ beta)} {B (\ alpha, \ beta)} = 1 - \ frac {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} $$

Je peux vérifier par ordinateur que cela fonctionne ...

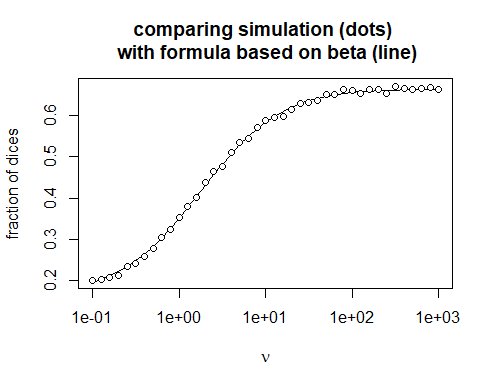
  ### calculer le résultat pour lancer un dé à n faces n fois
rolldice <- fonction (n, nu) {
  p <- rbeta (1, nu * 1 / n, nu * (n-1) / n)
  k <- rbinom (1, n, p)
  sur <- (k>0)
  en dehors
}

### calculer la moyenne d'un échantillon de dés
meandice <- fonction (n, nu, reps = 10 ^ 4) {
  somme (répliquer (reps, rolldice (n, nu))) / reps
}
meandice <- Vectoriser ((meandice))
### simuler et calculer la variance n

set.seed (1)
n <- 6
nu <- 10 ^ seq (-1,3,0.1)
y <- meandice (n, nu)
plot (nu, 1-beta (nu * 1 / n, n + nu * (n-1) / n) / beta (nu * 1 / n, nu * (n-1) / n), log = "x ", xlab = expression (nu), ylab =" fraction de dés ",
     main = "comparaison de la simulation (points) \ n avec une formule basée sur bêta (ligne)", main.cex = 1, type = "l")
points (nu, y, lty = 1, pch = 21, col = "noir", bg = "blanc")
 

.... Mais je n'ai aucun bon moyen de résoudre analytiquement l'expression pour $ n \ to \ infty $ .

Wavec le temps d'attente Cependant, avec les temps d'attente, je peux alors exprimer la limite de la distribution binomiale bêta (qui ressemble maintenant plus à une distribution bêta de Poisson) avec une variance du facteur exponentiel des temps d'attente.

Donc, au lieu de $ 1-e ^ {- 1} $ , nous recherchons $$ 1- \ int e ^ {- \ lambda} p (\ lambda) \, \ text {d} \, \ lambda $$ .

Maintenant, ce terme intégral est lié à la fonction génératrice de moment (avec $ t = -1 $ ). Donc, si $ \ lambda $ est distribué normalement avec $ \ mu = 1 $ et la variance $ \ sigma ^ 2 $ alors nous devrions utiliser:

$$ 1-e ^ {- (1- \ sigma ^ 2/2)} \ quad \ text {au lieu de} \ quad 1-e ^ {- 1} $$

Application

Ces lancers de dés sont un modèle de jouet. De nombreux problèmes de la vie réelle auront des variations et des situations de dés pas tout à fait équitables.

Par exemple, supposons que vous souhaitiez étudier la probabilité qu'une personne soit malade à cause d'un virus avec un certain temps de contact. On pourrait baser les calculs pour cela sur la base de certaines expériences qui vérifient la probabilité d'une transmission (par exemple, soit des travaux théoriques, soit des expériences de laboratoire mesurant / déterminant le nombre / la fréquence des transmissions dans une population entière sur une courte durée), puis extrapoler cette transmission à un mois entier. Supposons que vous constatiez que la transmission correspond à 1 transmission par mois et par personne, alors vous pourriez conclure que 1-1 $ / e \ environ 0,63 \% $ de la population recevra malade. Cependant, cela pourrait être une surestimation car tout le monde ne pourrait pas tomber malade / transmettre avec le même taux. Le pourcentage diminuera probablement.

Cependant, cela n'est vrai que si la variance est très grande. Pour cela, la distribution de $ \ lambda $ doit être très biaisée. Parce que, bien que nous l'ayons exprimé comme une distribution normale auparavant, les valeurs négatives ne sont pas possibles et les distributions sans distributions négatives n'auront généralement pas de grands ratios $ \ sigma / \ mu $ , sauf s'ils sont fortement biaisés. Une situation avec une inclinaison élevée est modélisée ci-dessous:

Nous utilisons maintenant le MGF pour une distribution de Bernoulli (l'exposant de celle-ci), car nous avons modélisé la distribution comme suit: $ \ lambda = 0 $ avec probabilité $ 1-p $ ou $ \ lambda = 1 / p $ avec probabilité $ p $ .

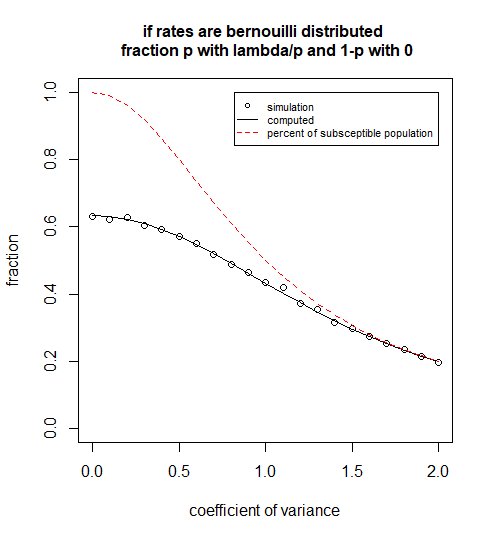
  set.seed (1)
taux = 1
temps = 1
CV = 1
### calculer le résultat de la maladie avec un taux variable
getsick <- fonction (taux, CV = 0,1, temps = 1) {
            ### tronquer les changements sd et mean mais pas beaucoup si CV est petit
  p <- 1 / (CV ^ 2 + 1)
  lambda <- rbinom (1,1, p) / (p) * taux
  k <- rpois (1, lambda * heure)
sur <- (k>0)
  en dehors
}


CV <- seq (0,2,0,1)
plot (-1, -1, xlim = c (0,2), ylim = c (0,1), xlab = "coefficient de variance", ylab = "fraction",
     cex.main = 1, main = "si les taux sont distribués en bernouilli \ n fraction p avec lambda / p et 1-p avec 0")
for (cv dans CV) {
  points (cv, somme (répliquer (10 ^ 4, getsick (rate = 1, cv, time = 1))) / 10 ^ 4)
}

p <- 1 / (CV ^ 2 + 1)
lignes (CV, 1- (1-p) -p * exp (-1 / p), col = 1)
lignes (CV, p, col = 2, lty = 2)

légende (2,1, c ("simulation", "calculé", "pourcentage de la population subsceptible"),
       col = c (1,1,2), lty = c (NA, 1,2), pch = c (1, NA, NA), xjust = 1, cex = 0,7)
 

La conséquence est. Supposons que vous ayez un $ n $ élevé et que vous n’ayez aucune possibilité d’observer des lancers de dés $ n $ (par exemple, il faut à long), et à la place vous filtrez le nombre de $ n $ lancers seulement pendant une courte période pour de nombreux dés différents. Ensuite, vous pouvez calculer le nombre de dés qui ont lancé un nombre $ n $ pendant ce court laps de temps et en vous basant sur ce calcul, ce qui se passerait pour $ n $ rouleaux. Mais vous ne sauriez pas à quel point les événements sont corrélés dans les dés. Il se peut que vous ayez affaire à une probabilité élevée dans un petit groupe de dés, au lieu d'une probabilité uniformément répartie entre tous les dés.

Cette «erreur» (ou vous pourriez dire simplification) se rapporte à la situation avec le COVID-19 où l'idée circule que nous avons besoin de 60% des personnes immunisées pour atteindre l'immunité collective. Cependant, ce n'est peut-être pas le cas. Le taux d'infection actuel n'est déterminé que pour un petit groupe de personnes, il se peut qu'il ne s'agisse que d'une indication de la contagiosité d'un petit groupe de personnes.

Simplifiez, puis étendez. Commencez avec une pièce de monnaie. Une pièce est un dé à 2 faces (S = 2).

L'espace de probabilité exhaustif est

T | H

Deux possibilités. On satisfait la condition de toutes les têtes. Donc, vos chances de gagner toutes les têtes avec une pièce (n = 1) sont de 1/2.

Essayez donc deux pièces (n = 2). Tous les résultats:

TT | TH | HT | HH

Quatre possibilités. Un seul correspond à vos critères. Il est à noter que la probabilité que l'un soit face et l'autre face est de 2/4 car deux possibilités des quatre correspondent à vos critères. Mais il n’existe qu’une seule façon d’obtenir toutes les têtes.

Ajouter une autre pièce (n = 3) ...

TTT | THT | HTT | HHT

TTH | THH | HTH | HHH

8 possibilités. Un seul répond aux critères - donc 1/8 de chances de toutes les têtes.

Le motif est (1 / S) ^ n ou (1/2) ^ 3.

Pour les dés S = 6, et nous en avons 6.

La probabilité d'obtenir un 6 sur un jet donné est de 1/6. Les rouleaux sont des événements indépendants. Donc, utiliser 2 dés pour obtenir les 6 équivaut à (1/6) * (1/6) ou 1/36.

(1/6) ^ 6 vaut environ 1 sur 46 656